Depth_First_Search

过程

  1. 从某个顶点v1出发，然后找到并访问与v1的邻接点（且从未访问过）v2，再从v2出发访问与v2相邻的顶点。–>这就是递归思想

  2. 直到所有的顶点被访问到。

  • 因为要记录该点是否被访问过，所以需要一个数组bool visited[MAXVEX];

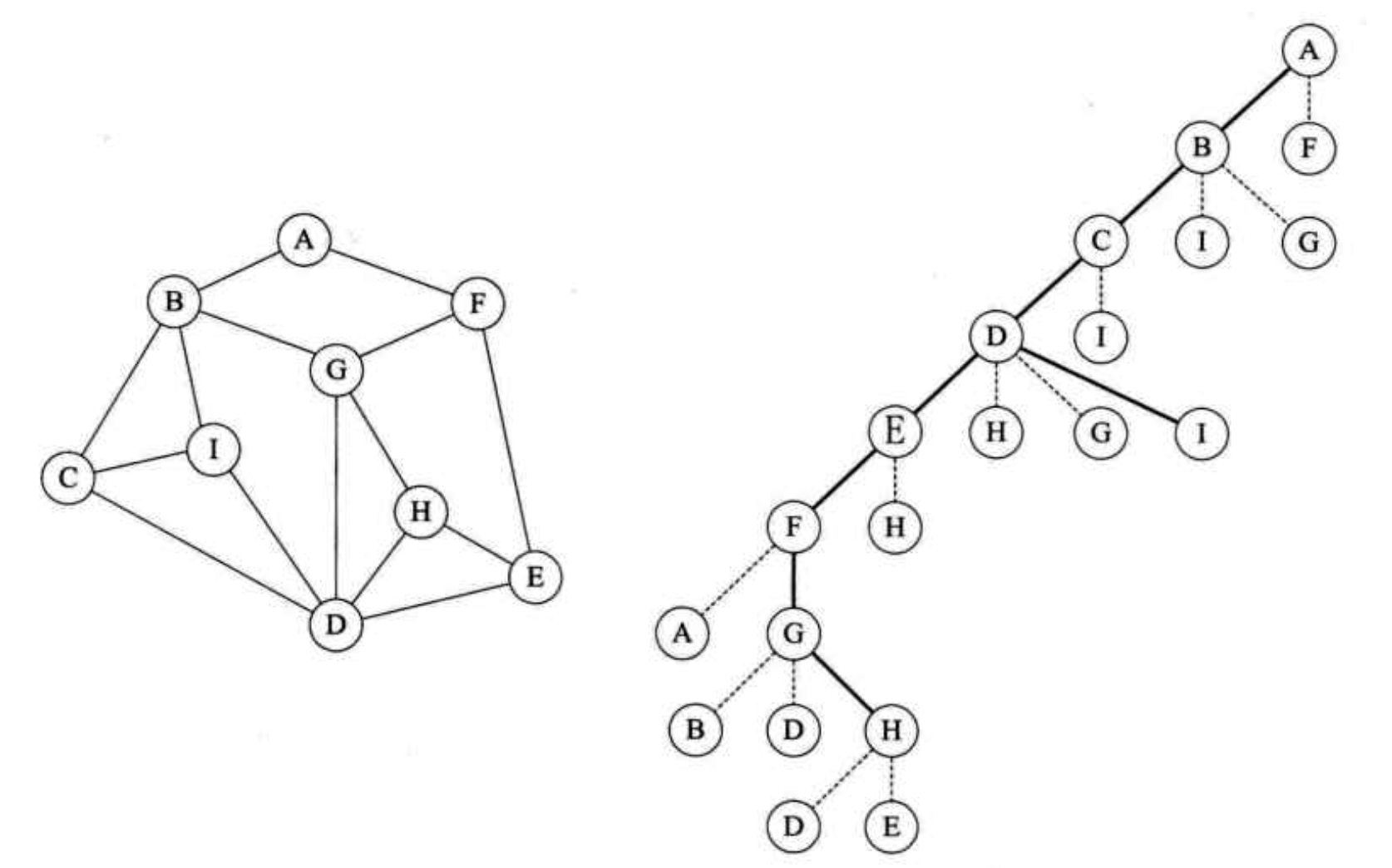
邻接矩阵遍历

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
void DFS(MGraph G, int i)
{
    int j;
    visited[i] = true;
    printf("%c ", G.vexs[i]);
    for(j = 0; j < G.numVertexs; j++)
    {
        //有边(i--j)，且 j 顶点没被访问
        if(G.arc[i][j] == 1 && visited[j] == false)
            DFS(G, j);
    }
}

void DFSTraverse(MGraph G)
{
    int i;
    for(i = 0; i < G.numVertexs; i++)
        visited[i] = false;
    for(i = 0; i < G.numVertexs; i++)
        if(visited[i] == false)
            DFS(G, i);
}

邻接表遍历

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
void DFS(GraphAdjList *G, int i)
{
    EdgeNode *p;
    visited[i] = true;
    printf("%c", G->adjList[i].data);
    p = G->adjList[i].firstedge;
    while (p)
    {
        if(!visited[p->adjvex])
            DFS(G, p->adjvex);
        p = p->next;
    }
    
}

void DFSTraverse(GraphAdjList *G)
{
    int i;
    for(i = 0; i < G->numVertexs; i++)
        visited[i] = false;
    for(i = 0; i < G->numVertexs; i++)
        if(!visited[i])
            DFS(G, i);
}

时间复杂度

  • 对比邻接矩阵和邻接表的遍历过程，可容易得出
    假如n个顶点，e条边
  1. 邻接矩阵：$O(n^2)$
  2. 邻接表：$O(n + e)$
  • 所以，对于多顶点少边的这种情况，邻接表不但节省了空间，还提高了函数的运行效率