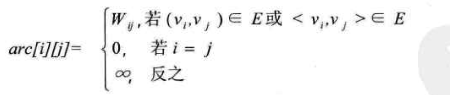前言

由于图的多方向性，不能用顺序存储结构来实现。如果我用多重链表的话，那么结构中的多个指针就会造成空间资源的浪费（因为图的顶点上的度是不确定的）。因此图的存储结构，不应该使用物理存储去实现。图的实现被提供了5种存储结构。1. 邻接矩阵 2.邻链表 3.十字链表 4. 邻接多重链表 5. 边集数组。

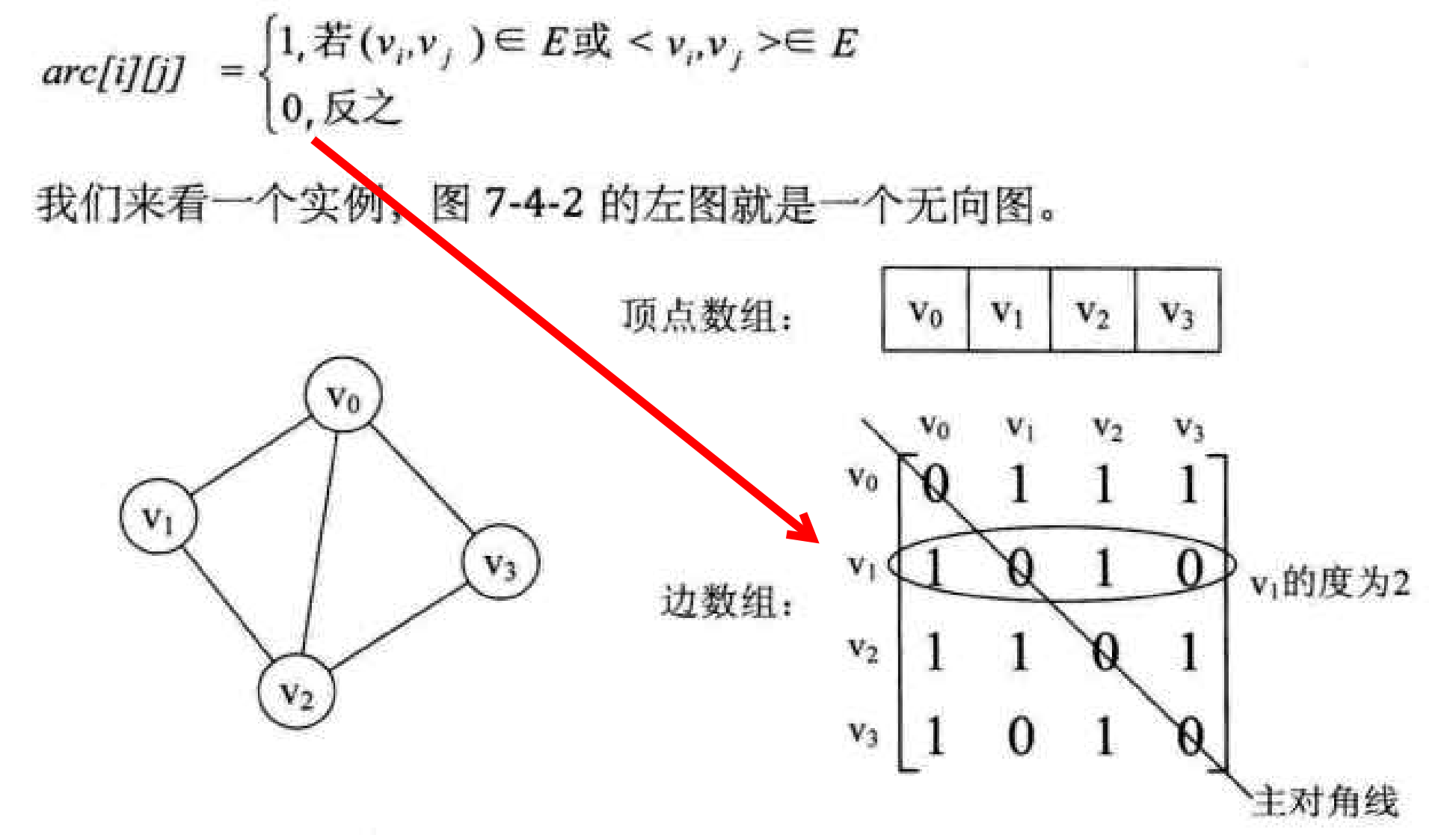
邻接矩阵

由顶点数组（一维）和边或弧数组（二维）组成

无向图

  1. 例如
    a[i][j]的0，1值表示，从i–j这个edge是否存在，1存在，0不存在。
    所以类似于a[i][i]这样的顶点到顶点的值都为0

  2. 无向图的边数组是一个对称矩阵，即满足a[i][j] == a[j][i]
    因为它是无向的，i–j不存在，则j–i也不存在。那么i–j存在，则，j–i也存在啊
    所以，在无向图中a[i][j]和a[j][i]无区别

  3. Vi的度就是把第i行（或列）的元素加起来

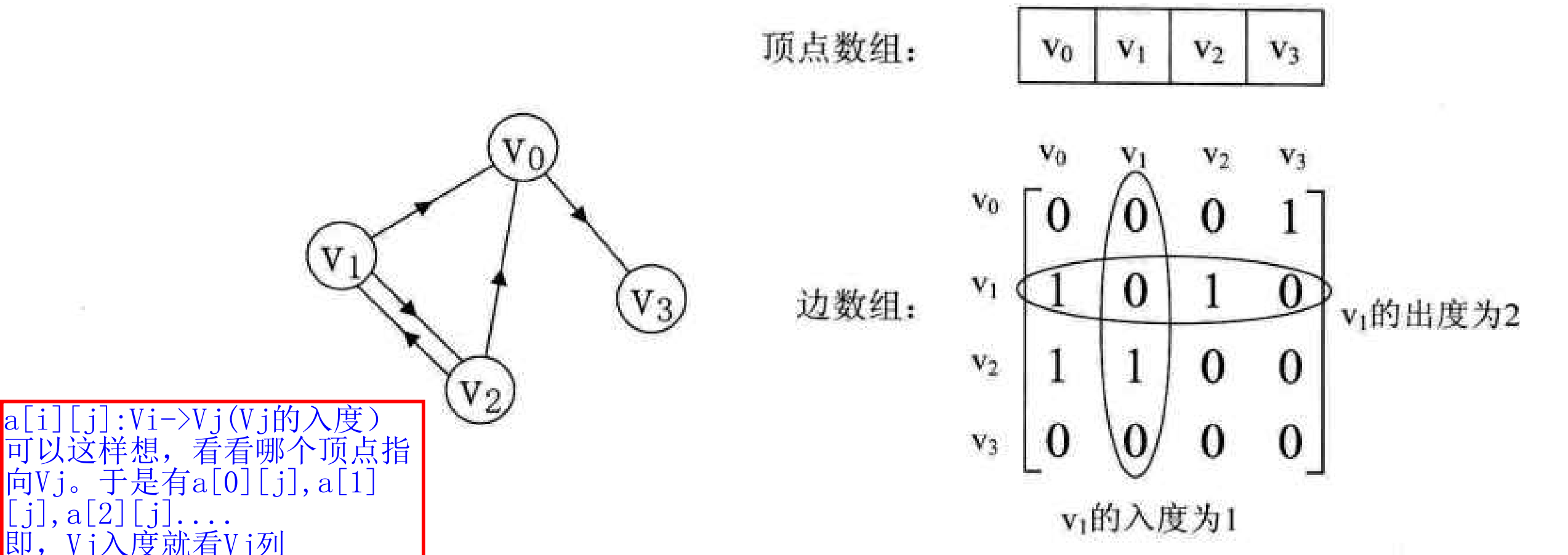
有向图

  1. 有向图就不是对称矩阵了。因为它们顶点的指向是有方向的，i–>j不一定j–>i。

  2. 出度和入度。有向图中，要研究这两个。只要知道前面的指向问题，就可以知道。Vi的出度是看矩阵中的行a[i]--[]，Vi的入度是看矩阵中的列a[]--[i]。将行或列加起来就是出度和入度的值了。

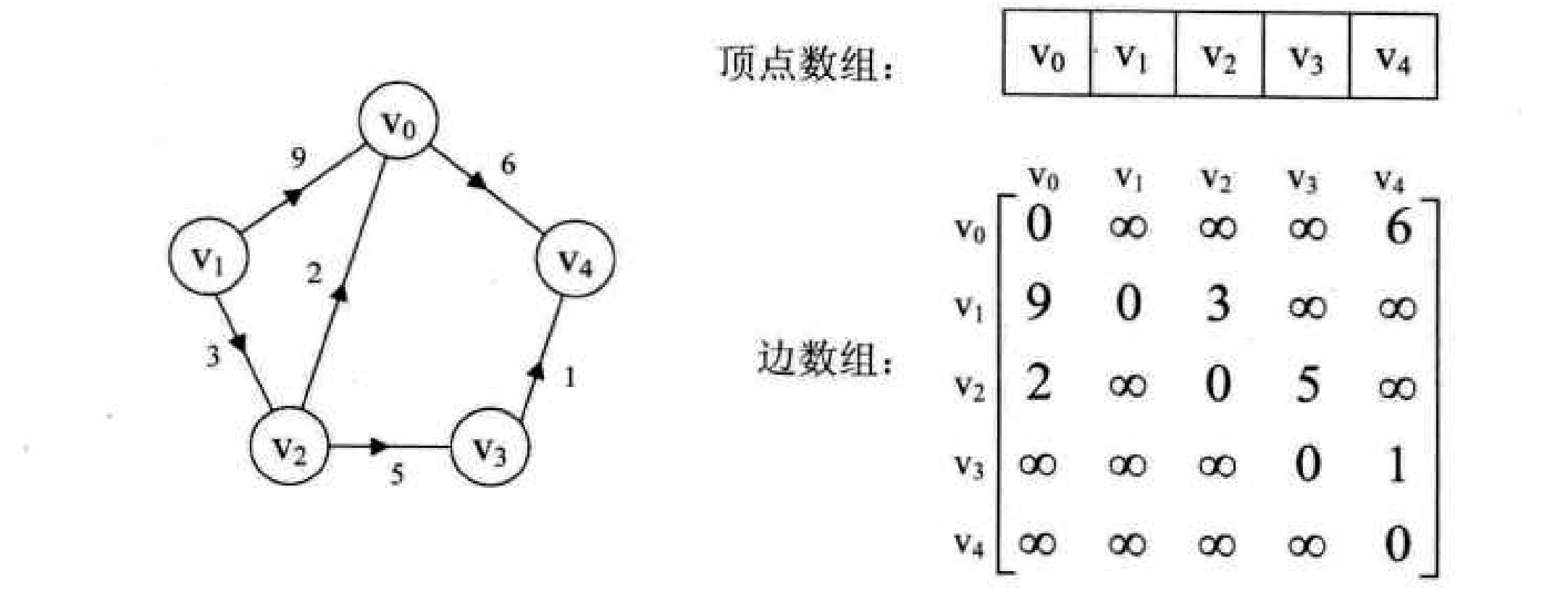
网Network

网就是每条edge上带有权的图

  1. 矩阵上的值

无向图的创建

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
#ifndef _Graph_H
#include <stdbool.h>
#include <stdio.h>
typedef char VertexType;//顶点类型
typedef int EdgeType;//边上的权类型
#define MAXVEX 100 //最大顶点数
#define INFINITY 65535 //用65535代表无穷大

bool visited[MAXVEX];

typedef struct 
{
    VertexType vexs[MAXVEX]; //顶点表
    EdgeType arc[MAXVEX][MAXVEX];//邻接矩阵，
    int numVertexs, numEldge;//顶点数，边数
}MGraph;

void CreateMGraph(MGraph *G);

void DFS(MGraph G, int i);

void DFSTraverse(MGraph G);
#endif
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
#include "graph.h"

void CreateMGraph(MGraph *G)
{
    int i, j, k, w;
    printf("Enter the number of Vertexs and edge:");
    scanf("%d %d", &G->numVertexs, &G->numEldge);
    printf("Enter the information of Vertexs array:");
    for(i = 0; i < G->numVertexs; i++)
        scanf(" %c", &G->vexs[i]);
    //初始化
    for(i = 0; i < G->numEldge; i++)
        for(j = 0; j < G->numEldge; j++)
            G->arc[i][j] = MAXVEX;
    
    for(k = 0; k < G->numEldge; k++)
    {
        printf("Enter double dimensional array indexs and weight of the edges:");
        scanf("%d %d %d", &i, &j, &w);
        G->arc[i][j] = w;
        G->arc[j][i] = G->arc[i][j];
    }
}

邻接表

邻接矩阵如果要处理顶点很多，而边很少的图那么会造成空间的浪费。所以，引入邻接表来避免这种现象发生。

  1. 结构数组。每个数组的元素是代表每个顶点。每个结构包含链表节点指针（firstedge），每个顶点类型（data(V1 ，V2))
1
2
3
4
5
typedef struct VertexNode        //顶点表节点
{
    VertexType data;
    EdgeNode *firstedge;
}VertexNode, AdjList[MAXVEX];
  1. 链表。每个节点包含顶点下标值（i（Vi）)，权值，指向下一个节点点指针（next）
1
2
3
4
5
6
typedef struct EdgeNode         //边表节点
{
    int adjvex;//邻接点域，用于存储对应顶点下标
    EdgeType weight;//用于存储权值
    struct EdgeNode *next;
}EdgeNode;
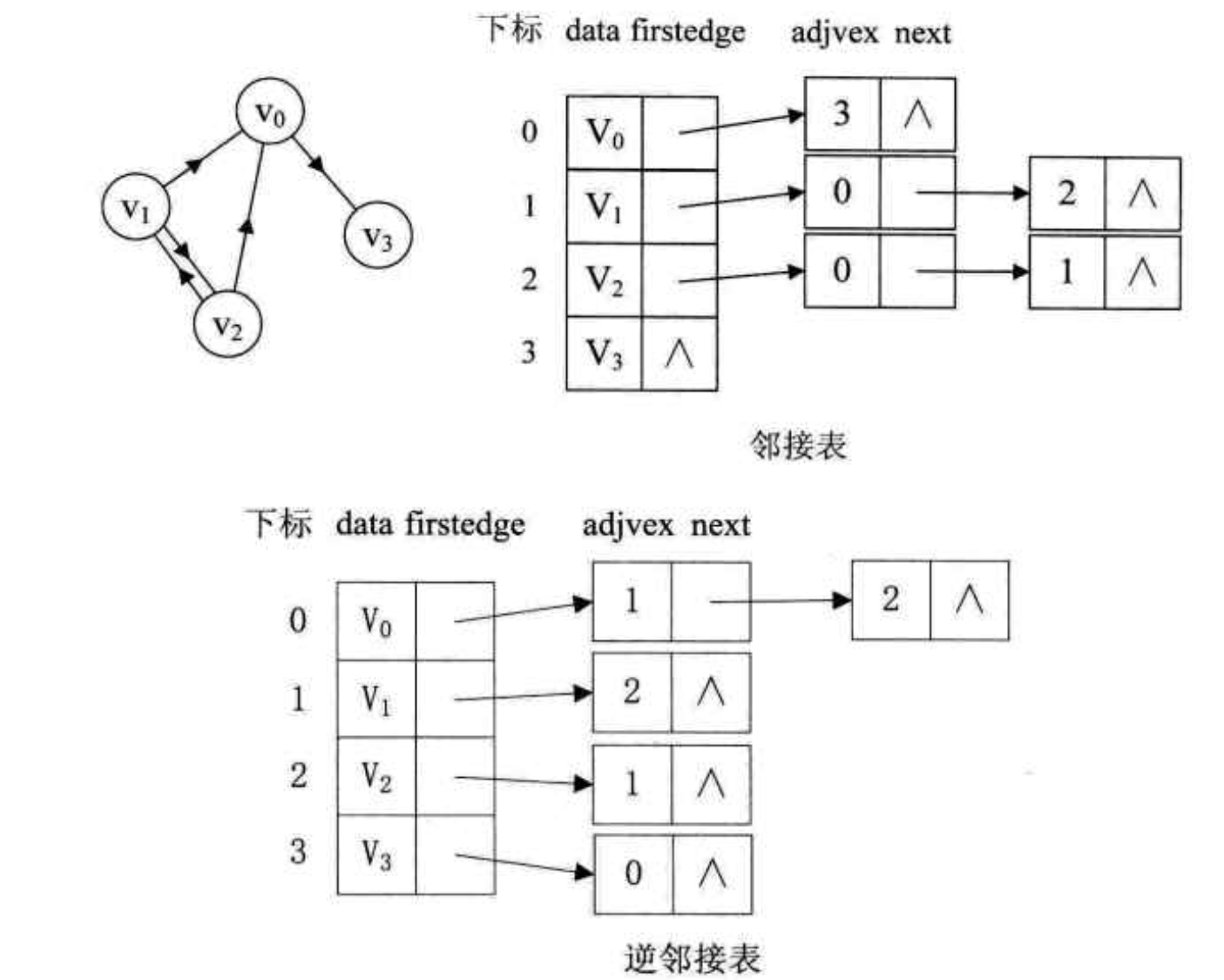
  • 然鹅，如果是面对有向图的话，因为弧有方向，所以有出度和入度。这样一来，这个邻接表，又可以分为两种。以弧头为链表的头（邻接表方便计算出度），以弧尾为链表的表头（逆邻接表方便计算入度）。

创建

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
#ifndef _List_H
#define MAXVEX 100
typedef char VertexType;
typedef int EdgeType;

typedef struct EdgeNode         //边表节点
{
    int adjvex;//邻接点域，用于存储对应顶点下标
    EdgeType weight;//用于存储权值
    struct EdgeNode *next;
}EdgeNode;

typedef struct VertexNode        //顶点表节点
{
    VertexType data;
    EdgeNode *firstedge;
}VertexNode, AdjList[MAXVEX];

typedef struct              //整个邻接表
{
    AdjList adjList;
    int numVertexs, numEdges;
}GraphAdjList;

void CreateAdjList(GraphAdjList *G);

#endif
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
#include<stdio.h>
#include<stdlib.h>
#include "list.h"

void CreateAdjList(GraphAdjList *G)
{
    int i, j, k;
    EdgeNode *e;
    printf("Enter the number of Vertexs and edges:");
    scanf("%d %d", &G->numVertexs, &G->numEdges);
    printf("Enter the elements of Vertexs List:");
    for(i = 0; i < G->numVertexs; i++)
    {
        scanf("%c", &G->adjList[i].data);
        G->adjList[i].firstedge = NULL;
    }
    for(k = 0; k < G->numEdges; k++)
    {
        printf("Enter the value of i and j with the edge(Vi,Vj):");
        scanf("%d %d", &i, &j);
        //生成节点Vj
        e = malloc(sizeof(EdgeNode));
        e->adjvex = j;
        //头插法
        e->next = G->adjList[i].firstedge;//将e指针指向当前顶点指向的节点
        G->adjList[i].firstedge = e;//将当前顶点指针指向e
        //生成节点Vi
        e = malloc(sizeof(EdgeNode));
        e->adjvex = i;
        e->next = G->adjList[i].firstedge;
        G->adjList[j].firstedge = e;

    }
}

十字链表

因为邻接表容易解决出度情况，要想了解入度就要遍历整个表才能知道。而逆邻接表也有这个情况。如果我们想要将两者的优势互补，就引入了十字链表。