概念

二叉树的遍历是从根节点出发，按照某几种不同的顺序遍历每个节点，使得每个节点被遍历仅一遍。
这些遍历方法分为：1. 前序遍历2. 中序遍历3. 后序遍历4. 层序遍历
规则：若树为空(T == NULL)，则空操作返回(return)，否则执行访问（递归）

说明

如何看待遍历顺序？

![(https://i.loli.net/2020/05/19/1W6rsVNP9hJubB8.png)

这张图已经完美说明了。首先，把这颗树加上空节点看成是完全二叉树，然后就它们的孩子嵌套并于括号括起来。

前序遍历

  • 打印顺序：父母。左子孙。右子孙。
1
2
3
4
5
6
7
8
void PreOrderTraverse(Tree T)
{
    if(T == NULL)
        return;
    printf("%c", T->e);
    PreOrderTraverse(T->lchild);
    PreOrderTraverse(T->rchild);
}

中顺遍历

  • 打印顺序：左子孙。父母。右子孙。
1
2
3
4
5
6
7
8
void InOrderTraverse(Tree T)
{
    if(T == NULL)
        return;
    PreOrderTraverse(T->lchild);
    printf("%c", T->e);
    PreOrderTraverse(T->rchild);
}

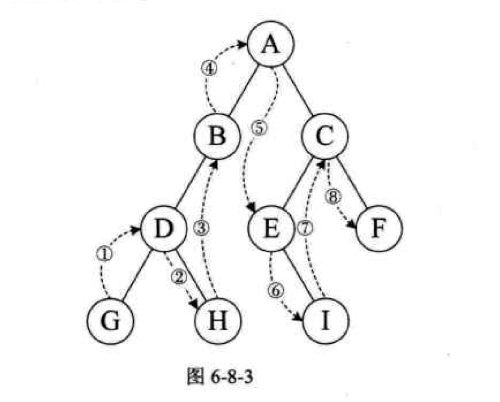
后序遍历

  • 打印顺序：左子孙。右子孙。父母。
1
2
3
4
5
6
7
8
void PostOrderTraverse(Tree T)
{
    if(T == NULL)
        return;
    PreOrderTraverse(T->lchild);
    PreOrderTraverse(T->rchild);
    printf("%c", T->e);
}

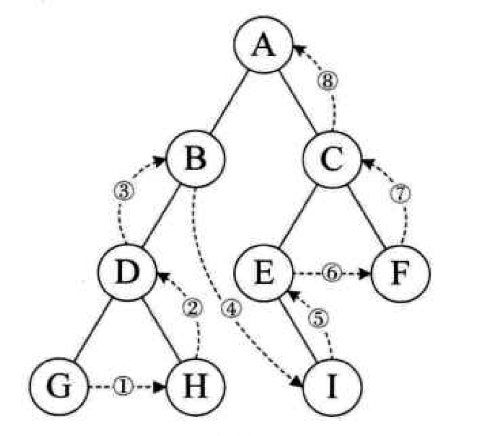
两个二叉树遍历性质

  1. 已知前序后序不能等到中序，也不能得到完整的二叉树

  2. 已知前序中序or中序后序能得到完整的二叉树。