前言

队列也是一种表。它把线性表限制了只能在第一项删除和最后一项添加数据。由此，它的结构–

指向头和尾的指针
每一项的数据
由于队列的删除和插入操作，需要移动数据而且时间复杂度为O(n)，但可以通过引入循环队列来使得时间复杂度变为O(1)

队列也同线性表类似，可以有两种存储结构。顺序存储结构和链式存储结构

顺序存储

说明

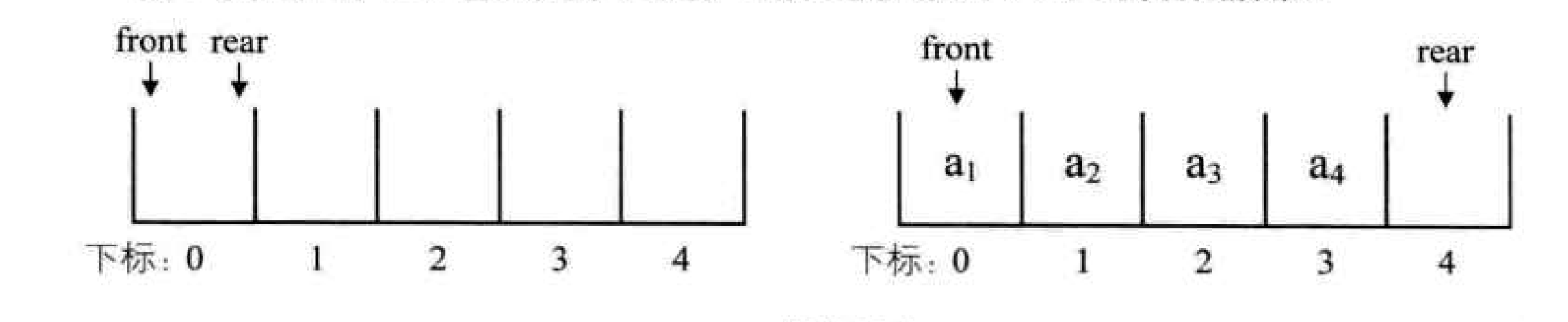
同样地，顺序存储结构用到数组来实现。结构中记录头和尾的指针其实是数组的下标(int)（front,rear)
注意，rear是指队尾元素的下一个位置，front是队头（第一个元素）

空队列的判断。所以，当rear == front的时候，不是还剩一个元素，而是空队列。（一个元素都没有）

当我们用循环队列的时候，如果，元素把整个数组都占满的时候，那么rear == front着个等式不是也成立吗？那么我们怎么区分满队列和空队列呢？我们应该采取一种方法—永远不要让元素占满整个数组。应该留一个空位。

满队列的判断。因为要留下一个位置不能用，要用Q->rear + 1 == Q->front判断队列为满
队列长度。因为队列是循环结构，所以可能会出现两段长度0 + rear 与 MAXSIZE - front。或一段长度rear - front
公式：r - f　　　r - f + M 得通用公式 (r - f + M) % M

循环的队列

因为队列只能在对头删除，队尾添加。如果一直这样操作下去。那么，我们定义的数组就会出现前面的项没有被使用，后面的项一直被占用。所以，为了有效的利用数组的空间。我们可以把着数组想象成环状。即，队头不一定要从数组的首元素开始，当要数据越界的时候将元素添加到数组的开头

EnQueue(),DeQueue()

在添加元素的时候，需要事先检查队列是否为满（元素是否占满数组）。
在删除元素的时候，需要事先检查队列是否为空。

实例

queue.h

#ifndef _Queue_h_
/*顺序存储结构的队列*/
#define MAXSIZE 5
#include <stdbool.h>
typedef int ElementType;

typedef struct 
{
    ElementType data[MAXSIZE];
    int front;
    int rear;
} Queue;

//初始化操作，建立一个空队列
void InitQueue(Queue *Q);
//将队列清空
void ClearQueue(Queue *Q);
//若队列为空返回true，否则返回false
bool IsEmpty(Queue *Q);
//若队列非空，用*e返回队列头元素
void GetHead(Queue *Q, ElementType *e);
//若队列存在，则插入元素到队列尾部
void EnQueue(Queue *Q, ElementType e);
//删除队列首元素，并用*e返回其值
void DeQueue(Queue *Q, ElementType *e);
//返回队列元素的个数
int QueueLength(Queue *Q);
//从队头至队尾依次对Q中的每个元素输出
void Traverse(Queue *Q);
//打印元素
void visit(ElementType e);

#endif

queue.c

#include<stdio.h>
#include<stdlib.h>
#include "queue.h"

void InitQueue(Queue *Q)
{
    Q->front = 0;
    Q->rear = 0;
}

void ClearQueue(Queue *Q)
{
    Q->front = 0;
    Q->rear = 0;
}

bool IsEmpty(Queue *Q)
{
    if(Q->rear == Q->front)
        return true;
    else
        return false;
}

void GetHead(Queue *Q, ElementType *e)
{
    if(Q->rear == Q->front)
    {
        fprintf(stderr, "The queue is empty");
        exit(1);
    }
    *e = Q->data[Q->front];
}

void EnQueue(Queue *Q, ElementType e)
{
    //因为数组是有界的，所有要判断队列是否为满
    if((Q->rear + 1) % MAXSIZE == Q->front)
    {
        fprintf(stderr, "Out of space.");
        exit(1);
    }
    Q->data[Q->rear] = e;   //记住，Q->rear是最后元素的下标+1
    Q->rear = (Q->rear + 1) % MAXSIZE;
    
}

void DeQueue(Queue *Q, ElementType *e)
{
    //队列可能为空，所以，要检查
    if(Q->front == Q->rear)
    {
        fprintf(stderr, "The queue is empty.");
        exit(1);
    }
    *e = Q->data[Q->front];
    Q->front = (Q->front + 1) % MAXSIZE;
}

int QueueLength(Queue *Q)
{
    return (Q->rear - Q->front + MAXSIZE) % MAXSIZE;
}

void Traverse(Queue *Q)
{
    int count = Q->front;
    while(count != Q->rear)
    {
        if(count >= MAXSIZE)
            count - MAXSIZE;
        printf("%d ", Q->data[count++]);
    }
    printf("\n");
}

void visit(ElementType e)
{
    printf("%d ", e);
}

顺序队列

前言

顺序存储

说明

循环的队列

EnQueue(),DeQueue()

实例